Metodi Numerici per ODEs

Come sarà il tempo domani?

L’operazione che effettuiamo per avere la risposta a questa domanda è “semplicemente” cercare le previsioni meteo su Google. Per il resto ci pensano i siti di meteorologia con qualche “magia”.

La predizione dei fenomeni fisici non è cosa affatto semplice e, in molti contesti, non siamo in grado di fornire una risposta esatta. Molto spesso siamo in grado di dare una risposta che si avvicina a quella esatta, ma non lo è. Molti fenomeni sono tuttora così complessi che non si hanno a disposizione modelli matematici in grado di predirne i comportamenti: se così fosse, potremmo predire i futuri terremoti oppure l’esatta traiettoria degli uragani senza alcuna incertezza.

Ovviamente non tutti i fenomeni fisici arrivano ad un tale livello di complessità e possono essere valutati tramite tecniche note, sia analitiche che numeriche. Il problema è che non è sempre possibile procedere per via analitica (ovvero riuscire a risolvere il problema su carta) ma è necessario usare il computer. Ma è fondamentale osservare una cosa: non è il computer che risolve il problema! Siamo noi (umani) che implementiamo modelli matematici di fenomeni fisici mentre il computer si limita a fare i conti!

Nel seguente articolo si discuterà di alcuni metodi numerici per “prevedere” il futuro, ovvero come è possibile risolvere equazioni differenziali ordinarie (ODEs, Ordinary Differential Equations). In particolare verranno descritti i seguenti metodi (o schemi):

Metodo di Eulero in Avanti o Metodo di Eulero Esplicito (Forward Euler Method)
Metodo di Eulero all’Indietro o Metodo di Eulero Implicito (Backward Euler Method)
Metodo dei Trapezi o Metodo di Crank-Nicolson

Introduzione al problema

Le equazioni differenziali si presentano ogniqualvolta sia neccessario esprimere un cambiamento o variazione. Non sono nella matematica ma in molti altri contesti della scienza, le quantità in studio sono descritte come rateo di variazione di altre quantità (ad esempio lo spostamento che è funzione del tempo).

Assumendo che non sia possibile risolvere una ODE analiticamente, si deve procedere per la via numerica, discretizzando il dominio in maniera opportuna con uno step (intervallo) fisso. Vi sono metodi in cui tale intervallo può non essere costante (metodi multistep) in cui quindi l’intervallo varia durante la risoluzione del metodo; per ora ci si limiterà alla classe più semplice.

L’idea di fondo per la risoluzione numerica delle ODE è la discretizzazione del dominio:

Si immagina di avere una funzione il cui andamento è mostrato nel grafico di sinistra. L’evoluzione della funzione al variare di $x$ è naturalmente continuo, non ci sono “buchi”; contrariamente nella figura a destra notiamo che ci sono dei salti. Tuttavia i due andamenti sono simili, se non coincidenti, ovvero un generico punto sul grafico di destra è contenuto nella curva del grafico di sinistra. Insomma, è come aver preso il grafico a sinistra e lo si è mangiato con un intervallo fisso $\Delta x$ .

Dal momento che nel seguito ci saranno svariate dimostrazioni e passaggi, si introduce la notazione che è stata adottata.

Definita una funzione $f(x)$ come quella riportata nella figura in alto a sinistra, a seguito della discretizzazione del dominio continuo attraverso un intervallo $\Delta x$ , si genera un nuovo dominio, formato da valori finiti di $x$ , ovvero si ottiene un intervallo finito. Ogni punto di tale intervallo è definito con $x_n$ dove la $n$ è un indice che va da $0$ a $N$ , che corrispondono agli estremi dell’intervallo. Nella figura in alto a destra si avrà quindi che

$x_0 = 0 \qquad x_N = 10$

quindi un generico step potrà essere definito con $x_n$ (ad esempio n=5), mentre il successivo a questo step sarà $x_{n+1}$ , invece il precedente $x_{n-1}$ . E’ solo un modo di numerare le posizioni del nuovo dominio, nulla di più.

Fin qui non si sono introdotti metodi numerici ma si è solo parlato di discretizzazione; facciamo adesso un passo in più.

Immaginiamo quindi di voler risolvere una generica ODE

$\begin{cases} y'(x) = - (y(x)-1)^2 \\ y(0)=2 \end{cases}$

Ci si trova di fronte ad una ODE non lineare (è presente un quadrato) e analiticamente potremmo avere difficoltà nel tentare di risolverla. Immaginiamo però di conoscere la soluzione perché qualcuno ce la fornisce.

$y(x) = \frac{1}{x+1}+1$

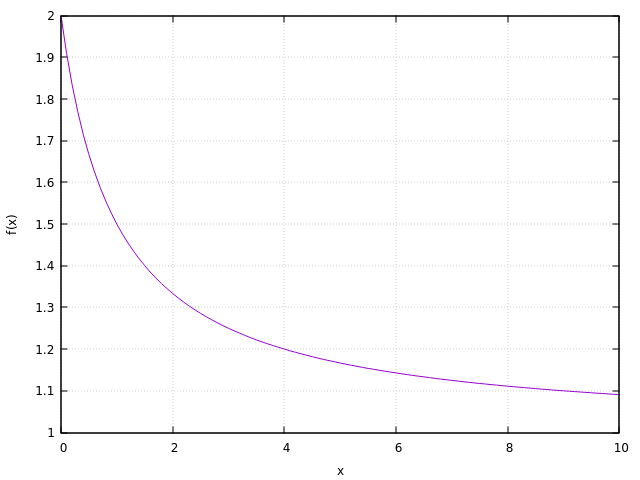
il cui andamento è mostrato nella seguente figura in un intervallo $x \in [0,10]$

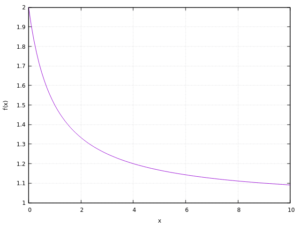
che è proprio la prima figura mostrato in precedenza.

In questo caso siamo stati fortunati perché conosciamo la soluzione. Ma se non sappiamo risolvere il problema analiticamente? Magari perché siamo imbranati in Analisi? Forse la numerica ci viene in aiuto…

Metodo di Eulero Esplicito

Il Metodo di Eulero Esplicito è probabilmente il metodo più semplice per poter risolvere una ODE; fu formulato nel 1768 ed è possibile trovarlo in numerose applicazioni a distanza di secoli. Lo schema esplicito è definito così:

(1) $y(x_{n+1}) = y(x_n) + f(x_n, y(x_{n}))$

Cerchiamo di comprendere la precedente equazione per quello che dice: si è in un dominio discretizzato e ciò è evidente dalla presenza dei valori puntuali del dominio, $x_n$ e $x_{n+1}$ . Sono presenti due funzioni, la $y$ e la $f$ , a loro volta definite in un contesto discreto. L’obiettivo è quello di valutare la $y$ in uno step successivo rispetto a quello in esame; per farlo è quindi necessario conoscere tutto ciò che è al secondo membro dell’equazione.

E’ importante notare che la precedente equazione non è casuale, ma proviene da una nota espansione, la Serie di Taylor: definita una generica funzione $f(x)$ , è possibile “ricreare” il comportamento di tale funzione, stabilito un intorno $x_0$ rispetto cui si sviluppa, ovvero:

$y(x) = y(x_0) + \frac{dy(x)}{dx}|_{x_0} (x - x_0) + \frac{1}{2} \frac{d^2y(x)}{d x^2}|_{x_0} (x-x_0)^2 + ...$

che in forma compatta è esprimibile come:

$y(x) = \sum_{k=0}^{\infty} \frac{y^{k}(x_0) (x-x_0)^k}{k!}$

dove la $y^k$ rappresenta la derivata k-esima (e non la potenza)

La particolarità della Serie di Taylor è che è valida anche se espressa in un contesto discreto. Del resto si è in grado di definire il comportamento di una funzione ad uno step $x_{n+1}$ espandendo in uno intorno $x_{n}$ . Matematicamente non si sta effettuando alcuna approssimazione, è semplicemente ciò che si è scritto prima, solo che al posto di $x$ e $x_0$ ci sono $x_{n+1}$ e $x_{n}$ :

(2) $y(x_{n+1}) = y(x_{n}) + \frac{dy}{dx}|_{x_n} (x_{n+1} - x_{n}) + \frac{1}{2} \frac{d^2y}{d x^2}|_{x_n} (x_{n+1}-x_{n})^2 + ...$

Fintanto che si considerano infiniti termini della sommatoria, il valore della $f(x_{n+1})$ è esatto, non è assolutamente approssimato. Altra semplificazione che è possibile fare per non appesantire le equazioni è ricordare che lo step tra un valore generico $x_{n+1}$ e $x_{n}$ è fisso, quindi lo si definisce come:

$\Delta x = x_{n+1}- x_{n}$

ciò permette di riscrivere l’equazione (2) in maniera più semplice

$y(x_{n+1}) = y(x_{n}) + \frac{dy}{dx}|_{x_n} \Delta x+ \frac{1}{2} \frac{d^2y}{d x^2}|_{x_n} \Delta x^2 + ...$

Il passo aggiuntivo che si fa è approssimare: si decide di troncare al 1° ordine l’espansione in Serie di Taylor, dal momento che vogliamo un’equazione lineare (ciò non toglie che potremmo troncare ad ordini superiori, ma non si giungerebbe allo Schema di Eulero Esplicito):

$y(x_{n+1}) = y(x_{n}) + \frac{dy}{dx}|_{x_n} \Delta x$

Si nota già una forte somiglianza con la (1) equazione. Infatti, ricordando che la ODE generica che si vuole studiare ha la seguente forma:

$\frac{dy(x)}{dx} = f(x,y(x))$

allora basta sostituire alla derivata proprio la $f$ , ottenendo:

$y(x_{n+1}) = y(x_{n}) + f(x_n, y(x_{n})) \Delta x$

Si è tornati alla definizione di Schema (o Metodo) di Eulero Esplicito (1).

Vediamo di applicarlo al problema differenziale di partenza:

$\frac{dy(x)}{dx}= - (y(x)-1)^2$

Si procede con la discretizzazione dell’equazione, come già fatto in precedenza, ricordando che la derivata è approssimabile con un rapporto finito:

$\frac{y(x_{n+1}) - y(x_{n})}{\Delta x}= - (y(x_n)-1)^2$

La si riscrive in modo tale da far apparire lo Schema di Eulero Esplicito.

$y(x_{n+1}) = y(x_n) - (y(x_n)-1)^2 \Delta x$

Si sarebbe potuto giungere allo stesso risultato andando a sostituire la derivata nello Schema di Eulero Esplicito al posto della $f$ , come fatto nella dimostrazione precedente. Entrambi gli approcci vanno bene. Di seguito si riporta un codice Fortran 95 e Matlab per l’implementazione dello schema: al posto della variabile indipedente $x$ è stata usata la $t$ , ma l’idea rimane la stessa (sono sempre lettere, le si possono chiamare come ci pare). I grafici presenti nell’articolo sono tutti relativi al codice Fortran 95.

program expliciteuler
implicit none
integer :: i, N
real :: y, dt , tf
real,external :: f
open (unit =1, file =" data .txt ",status ="new")

! Needed step to evaluate the solution . It must to be lesser than 1
! for convergernce analysis
dt = 0.1

! Final time
tf = 10

! Counter
N = tf/dt

! Initial Condition y(0)=2
y = 2
! Writing the first condition in a data file
write (1 ,*) 0.0 , 2.0
do i=1,N
    y = y + dt * f(y, (i - 1) * dt)
    write (1 ,*)i *dt , y
end do
end program

! The function to be solved , in this case the t is not explicit
real function f(y, t)
implicit none
real , intent (in) :: y, t
f = -y*y + 2*y -1
end function

function [t,y] = explicit_euler(t0,y0,t_end,h,fcn)

n = fix((t_end-t0)/h)+1;
t = linspace(t0,t0+(n-1)*h,n)';
y = zeros(n,1);
y(1) = y0;
for i = 2:n
  y(i) = y(i-1) + h*feval(fcn,t(i-1),y(i-1));
end

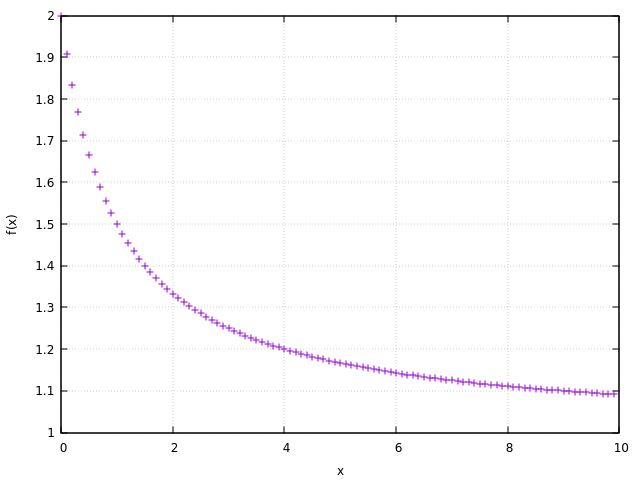
Andiamo a graficare ciò che il codice ci fornisce; in particolare lo si grafica andando a scegliere uno step $\Delta x = 0.1$ (nel codice Fortran 95 è il dt). Plottando si ottiene la seguente figura:

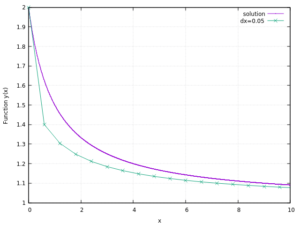Come primo tentativo non è male: in fin dei conti abbiamo ottenuto una nuova curva che assomiglia a quella esatta, con una piccola differenza di valore iniziale della $y(x)$ . Dal momento che possiamo modificare il passo di quanto vogliamo (apparentemente), grafichiamo un insieme di curve con $\Delta x$ differenti, ottenendo così la seguente figura:

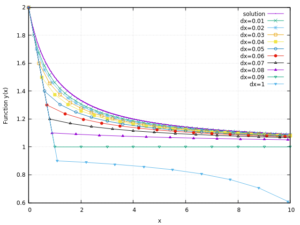
CI si accorge che in fin dei conti non possiamo modificare il $\Delta x$ di quanto vogliamo, perché raggiunto un certo valore, la soluzione numerica diverge da quella esatta. Cosa significa questo?

La convergenza dello schema è valida fintanto che viene rispettata la seguente equazione:

$|1 + \lambda \Delta x| < 1$

dove $\lambda$ , in generale, appartiene a $\mathbb{C}$ (insieme dei numeri complessi) e il suo valore dipende dal problema in esame.

Ma come si valuta il $\lambda$ ? Bisogna fare uno step in più.

Assoluta Stabilità (A-Stability) per Eulero Esplicito

Ciò che accomuna tutti i metodi numerici è la necessità di rispettare il criterio di convergenza (che cambia da metodo a metodo) e per far ciò è necessario introdurre il concetto di Assoluta Stabilità.

L’Assoluta Stabilità (o A-Stability) definisce il comportamento dello schema nella risoluzione di una generica ODE e permette di stabilire quale sia il limite di $\Delta x$ che non possiamo superare. Qualora superassimo il limite, la soluzione numerica divergerebbe da quella esatta, quindi avremmo applicato in maniera scorretta uno schema. Per risolvere questo problema, dobbiamo introdurre la linear test equation (equazione test lineare) che permetterà di valutare $\lambda$ :

$\begin{cases} y'(x) = \lambda y \\ y(0) = y_0 \end{cases}$

che è una generica ODE lineare, mentre $y_0$ è un valore nel punto $x_0$ iniziale. La esatta soluzione, analitica, è:

$y(x) = y_0 e^{\lambda x}$

Se il $\lambda <0$ , studiando il limite della soluzione:

$\lim_{x\rightarrow\infty} y(x) = \lim_{x\rightarrow\infty} y_0 e^{\lambda x} \rightarrow 0$

Ad esempio, se abbiamo una soluzione del tipo $y(x) = 10 \, e^{\lambda x}$ con $\lambda = -0.3$ avremo questo andamento.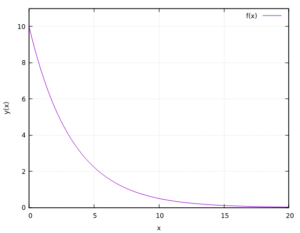

Quindi il limite per $x\rightarrow \infty$ ci sta dicendo di andare a valutare la soluzione per un valore molto grande dell’ascissa. GIà dopo $x=15$ la soluzione è praticamente piatta sullo 0, quindi il limite tende a 0.

Osservazione: non confondete quest’ultimo grafico con la soluzione esatta o numerica dell’equazione differenziale di partenza. E’ un caso che gli andamenti delle soluzioni sono entrambi decrescenti; se avessimo preso un’altra ODE da studiare, la sua soluzione potrebbe ad esempio essere un esponenziale che cresce fino alla convergenza ad un dato valore.

Ora che abbiamo capito cosa è la linear test equation, si riprende lo Schema di Eulero Esplicito:

$y(x_{n+1}) = y(x_n) + f(x_n, y(x_{n}))$

Durante la dimostrazione dello schema tramite la Serie di Taylor si era sostituita la funzione $f(x_n, y(x_n))$ con la con la derivata $y'$ (perché appunto sono la stessa cosa), quindi si fa questo passaggio utilizzando $y'(x) = \lambda y$ :

$y(x_{n+1}) = y(x_n) + \lambda y(x_n) = y(x_n) \, (1+\lambda \Delta x)$

dove nell’ultimo passaggio si sono solo raggruppati i termini.

A questo punto, però, si può notare una cosa: si è scritta la precedente equazione tra lo step $n+1$ e $n$ . Ma se si tornasse indietro fino a che lo step $n$ fosse quello iniziale $0$ ? Bene, procedendo con questa idea si ottiene questo:

$y(x_{n+1}) = y(x_n) + \lambda y(x_n) = y(x_n) \, (1+\lambda \Delta x) = y(x_{n-2}) \, (1 + \lambda \Delta x)^2 = y(x_{n-3}) \, (1 + \lambda \Delta x)^3 = ...$

$y(x_{n+1}) = y(x_0) (1 + \lambda \Delta x)^n$

Non notate una certa somiglianza con quello che si è scritto prima?

$y(x) = y_0 e^{\lambda x} \qquad \qquad y(x_{n+1}) = y_0 (1 + \lambda \Delta x)^n$

Certo, la prima è una soluzione esatta… ma finchè non consideriamo un dominio discretizzato anche la seconda equazione è esatta ( $x_{n+1}$ lo si può considerare come un punto di un dominio continuo). A breve si dimostrerà che affinché la soluzione numerica tenda a quella esatta deve avvenire che

$|1+ \lambda \Delta x| <1$

Siamo giunti alla condizione di Assoluta Stabilità per il Metodo di Eulero Esplicito.

Ma come si traduce questa condizione?

Il $\lambda$ è in generale un numero complesso ovvero $\lambda \in \mathbb{C}$ ; infatti, la soluzione di una generica ODE potrebbe avere una soluzione armonica, quindi definita da seni/coseni (ovvero da un esponenziale in cui appare un $\lambda$ complesso). Pertanto la condizione precedente deve essere intesa in un contesto complesso: ciò significa che la condizione è rispettata solo se il prodotto $\lambda \Delta x$ si trova all’interno del cerchio di centro (-1,0).

$\mathcal{D} = \{ z \in \mathbb{C}: |1 + z| <1 \}$

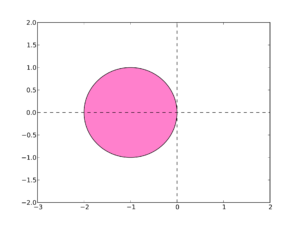
dove appunto $z=\lambda \Delta x$

Ok ma chi ce l’ho dà il $\lambda$ ? Anche qui si dimostrerà a breve che la $\lambda$ è pari a:

$\lambda = \frac{d f(x_0, y(x_0))}{dy}$

Per dimostrarlo dovremo fare un ultimo passo, che in realtà non aggiunge nulla di nuovo rispetto a ciò che è stato detto finora. SI riparte dalla linear test equation:

$\begin{cases} y'(x) = \lambda y \\ y(0) = y_0 \end{cases}$

e si era già vista la rispettiva soluzione

$y(x) = y_0 e^{\lambda x}$

Si utilizza nuovamente l’espansione in Serie di Taylor attorno al punto generico $x=x_0$ :

$f(x,y(x)) = f(x_0, y(x_0)) + \frac{d f(x_0,(y(x_0))}{dy} (y(x) - y(x_0)) + ...$

Troncando la serie al I ordine (quindi si prendono i termini prima dei puntini) e definendo:

$u(x) = y(x) - y(x_0)$

$\alpha = \frac{d f(x_0,(y(x_0))}{dy}$

$\lambda = \frac{d f(x_0,y(x_0))}{dy}$

SI giunge all’ODE generalizzata:

$u'(x) = \lambda u(x) + \alpha$

dove, dal momento che nello studio della Assoluta Stabilità si considera solo la differenza di soluzioni, si può trascurare l’addendo $\alpha$ , ri-ottenendo la linear test equation se $y(x) = u(x)$ . Insomma, alla fine in questa dimostrazione ci interessa la definizione del $\lambda$ ma è stato necessario sviluppare tutti questi passaggi per tornare al punto di partenza.

A questo punto si hanno tutti gli strumenti necessari per l’applicazione dello Schema di Eulero Esplicito.

Metodo di Eulero Implicito

Dopo aver compreso lo Schema di Eulero Esplicito, si passa ai metodi impliciti che creano sempre problemi agli studenti.

Il Metodo di Eulero Implicito è esprimibile come:

(4) $y(x_{n+1}) = y(x_n) + f(x_{n+1}, y(x_{n+1}))$

A questo punto una domanda sorge spontanea: come faccio a trovare il valore della funzione nel passo successivo $y_{n+1}$ se per trovarlo devo conoscere la funzione $f$ tramite $y_{n+1}$ ? Questo dubbio verrà spiegato in seguito… per ora effettuiamo le stesse considerazioni fatte per lo Schema di Eulero Esplicito.

Si dimostra lo Schema di Eulero Implicito: anche qui si riparte dall’espansione in Serie di Taylor: come detto prima, definita una generica funzione $f(x)$ , è possibile “ricreare” il comportamento di tale funzione, stabilito un intorno $x_0$ rispetto cui si sviluppa, ovvero:

$y(x) = y(x_0) + \frac{dy(x)}{dx}|_{x_0} (x - x_0) + \frac{1}{2} \frac{d^2y(x)}{d x^2}|_{x_0} (x-x_0)^2 + ...$

per cui si è anche detto che l’espansione è valida anche se espressa in un contesto discreto. La differenza rispetto al caso precedente è che, sebbene si vada sempre a troncare al I ordine, il punto scelto in cui si effettua l’espansione non è un punto precedente ma un punto successivo, ovvero:

$y(x_{n}) = y(x_{n+1}) + \frac{dy}{dx}|_{x_{n+1}} (x_{n} - x_{n+1}) + \frac{1}{2} \frac{d^2y}{d x^2}|_{x_{n+1}} (x_{n}-x_{n+1})^2 + ...$

che troncata al I ordine ed imponendo l’uguaglianza (e non l’approssimazione):

$y(x_{n}) = y(x_{n+1}) + \frac{dy}{dx}|_{x_{n+1}} (x_{n} - x_{n+1})$

riscrivibile anche come

$y(x_{n}) = y(x_{n+1}) - \frac{dy}{dx}|_{x_{n+1}} (x_{n+1} - x_{n})$

dove anche qui, ricordando la definizione di $\Delta x$ , si nota la somiglianza con la (4) equazione. Quindi possiamo dire che

$\frac{dy}{dx}|_{x_{n+1}} = f(x_{n+1}, y(x_{n+1}))$

da cui, spostando il termine con la derivata/funzione al primo membro, si riottiene:

$y(x_{n+1}) = y(x_n) + f(x_{n+1}, y(x_{n+1}))$

Avendo dimostrato il metodo, l’applicazione alla ODE di partenza segue l’approccio dello Schema di Eulero Esplicito. Ma rimane il problema della funzione al secondo membro: come faccio a calcolare la funzione se è definita dalla stessa incognita che cerco? In realtà il problema non si risolve rimanendo nello Schema di Eulero Implicito, ma si utilizza un predittore esplicito (Explicit Predictor): ogni volta che iteriamo per risolvere lo schema implicito, è necessario prima applicare un metodo esplicito che ci fornisca $y_{n+1}$ (ad esempio lo Schema di Eulero Esplicito, ma ce ne sono altri).

Di seguito verranno presentati due script, uno Fortran 95 e l’altro Matlab, che seguono in linea di principio il seguente schema:

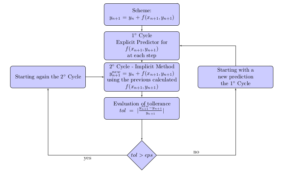
program euleroimplicito

    implicit none
    integer :: i, N, tf
    real :: dt, eps, tol, fnew, ynew, del
    real, external :: fu
    real, allocatable :: f(:), y(:)
    open(unit=1,file="data3.txt",status="new") 	

    eps = 0.01

    tf = 1
    dt = 0.01

    N = int(tf/dt)

    allocate(f(N))
    allocate(y(N))

    y(1) = 2.0
    write(1,*) 0, 2.0

    do i=2,N
	f(i) = fu(y(i-1), (i - 1) * dt)
        y(i) = y(i-1) + dt * f(i)
	write(1,*) i*dt, y(i)

	tol = 1.0
	do while (tol > eps)
		fnew = fu(y(i), i*dt) 
		ynew = y(i-1) + dt * fnew
                tol = abs((ynew-y(i))/y(i))
		y(i) = ynew
		f(i) = fnew
	end do
    end do

      deallocate(f)
      deallocate(y)


end program

! f(y,t): si inserisce la funzione che poi viene richiamata sopra
real function fu(y, t)
    implicit none
    real, intent(in) :: y, t

    fu = -y*y + 2*y -1 
end function

function [t,y,flag]=eulero_implicito(t0,y0,t_end,h,fcn,tol)
flag=0;

max_count=100;

n = fix((t_end-t0)/h) + 1;
t = linspace(t0,t0+(n-1)*h,n)';
y = zeros(n,1); y(1) = y0;
for i=2:n 
  yt1 = y(i-1) + h*feval(fcn,t(i-1),y(i-1));
  count = 0;  diff = 1;
  while diff(end) > tol && count < max_count
    yt2 = y(i-1) + h*feval(fcn,t(i),yt1);
    diff(count+1) = abs(yt2-yt1); 
    yt1 = yt2;
    count = count +1;
  end
  
  if count >= max_count
      flag=1;
  end
  y(i) = yt2;
end

Assoluta Stabilità (A-Stability) per Eulero Implicito

Anche per lo Schema di Eulero Implicito è fondamentale lo studio della convergenza. Prima di effetuarne la dimostrazione, possiamo dire che lo schema risulta assolutamente stabile se è rispettata la seguente disuguaglianza:

$|\frac{1}{1 - \lambda \Delta x}| < 1$

Notiamo quindi che il criterio di convergenza è un po’ diverso da quello dell’Eulero Esplicito. Anche qui dimostriamo tale disuguaglianza ripartendo dalla linear test equation (i primi passi sono gli stessi del caso Esplicito):

$\begin{cases} y'(x) = \lambda y \\ y(0) = y_0 \end{cases}$

generica ODE lineare, la cui esatta soluzione, analitica, è:

$y(x) = y_0 e^{\lambda x}$

Se il $\lambda <0$ , studiando il limite della soluzione:

$\lim_{x\rightarrow\infty} y(x) = \lim_{x\rightarrow\infty} y_0 e^{\lambda x} \rightarrow 0$

A questo punto si riprende lo Schema di Eulero Implicito:

$y_{n+1} = y_n + f(x_{n+1}, y(x_{n+1})) \Delta x$

Durante la dimostrazione dello schema tramite la Serie di Taylor, si era sostituita la funzione $f(x_{n+1}, y(x_{n+1}))$ con la derivata $y'(x)$ :

$y_{n+1} = y_n + \lambda y(x_{n+1}) \Delta x$

dove, raggruppando al primo membro il termine $y_{n+1}$ e poi dividendo tutto per $1 - \lambda \Delta x$ si giunge a:

$y_{n+1} = \frac{1}{1-\lambda \Delta x} y_n$

Come fatto in precedenza, anche qui si nota che l’equazione è stata scritta tra uno step $n+1$ e uno step $n$ , quindi si torna indietro fino allo step $0$ :

$y_{n+1} = \frac{1}{1-\lambda \Delta x} y_n = (\frac{1}{1-\lambda \Delta x})^2 y_{n-1} = ... = (\frac{1}{1-\lambda \Delta x})^n y_0$

dove si nota, anche qui, la somiglianza tra i seguenti:

$y(x) = y_0 e^{\lambda x} \qquad \quad y_{n+1} = y_0 (\frac{1}{1-\lambda \Delta x})^n$

Per lo stesso ragionamento fatto nel caso dell’Eulero Esplicito, il $\lambda$ è in generale un numero complesso ovvero $\lambda \in \mathbb{C}$ . Affinché la condizione di convergenza precedente sia rispettate allora il valore del $\lambda$ deve essere esterno al cerchio di raggio unitario e di centro (1,0) nel piano complesso.

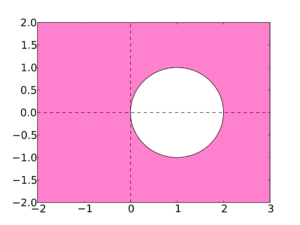
ovvero si ha il caso (quasi) opposto di Eulero Esplicito; si deve rimanere nel dominio ed esterni al cerchio,

$\mathcal{D} = \{ z \in \mathbb{C}: |\frac{1}{1-\lambda \Delta x}| <1 \}$

dove appunto $z=\lambda \Delta x$

I ragionamenti per la valutazione di $\lambda$ sono gli stessi effettuati per lo Schema di Eulero Esplicito quindi evito di riportare lo stesso procedimento qui di seguito.

Metodo dei Trapezi o Metodo di Crank-Nicolson

Un altro metodo molto utilizzato è quello di Crank-Nicolson; si tratta sempre di uno schema implicito, quindi può essere trattato come l’Eulero all’Indietro. Non si farà alcuna dimostrazione di questo schema per non appesantire l’articolo ma si daranno solo i risultati fondamentali per la sua implementazione. In particolare, è chiamato “metodo dei trapezi” poiché esso è definito nella seguente maniera:

(5) $y_{n+1} = y_n + \frac{\Delta x}{2} [f(x_n, y_n) + f(x_{n+1},y_{n+1})]$

dove al secondo membro della ODE è presente un’espressione che ricorda, appunto, l’area di un trapezio ( $(B+b) \cdot h/ 2$ ).

Anche in questo caso, trattandosi di uno schema implicito, è necessario utilizzare un Predittore Esplicito che possa fornire ad ogni iterazione un guess sulla quantità $y_{n+1}$ cosicché lo schema possa procedere. In generale tale metodo segue i passi riportati nel flow chart:

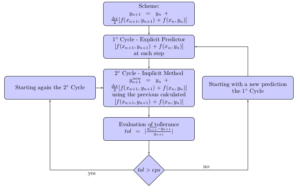
Anche qui si riporta un codice Fortran 95 per l’implementazione in cui il predittore esplicito è sempre quello di Eulero.

program cranknicolson

    implicit none
    integer :: i, N, tf
    real :: dt, eps, tol, fnew, ynew
    real, external :: fu
    real, allocatable :: f(:), y(:)
    open(unit=1,file="data6.txt",status="new") 	

    eps = 0.01
    tf = 1
    dt = 0.01

    N = int(tf/dt)

    allocate(f(N))
    allocate(y(N))


    y(1) = 2.0
    write(1,*) 0, 2.0
    i=1
    y(2) = y(1) + dt * fu(y(1),i*dt) 
				
    do i=2,N
	f(i) = (fu(y(i-1), (i-1)*dt) + fu(y(i), i*dt)) 
        y(i) = y(i-1) + 0.5*dt*f(i)
	write(1,*) i*dt, y(i)
	tol = 1.0
	do while (tol > eps)
		fnew = (fu(y(i-1), (i-1)*dt) + fu(y(i), i*dt)) 
		ynew = y(i-1) + 0.5*dt*fnew
		tol = abs((ynew-y(i))/y(i))
		y(i) = ynew
		f(i) = fnew
	end do
    end do

      deallocate(f)
      deallocate(y)


end program

! f(y,t): si inserisce la funzione che poi viene richiamata sopra
real function fu(y, t)
    implicit none
    real, intent(in) :: y, t

    fu = -y*y + 2*y -1 
end function

Per ulteriori approfondimento, consiglio il seguente corso del MIT.

Come sarà il tempo domani?

Introduzione al problema

Metodo di Eulero Esplicito

Assoluta Stabilità (A-Stability) per Eulero Esplicito

Metodo di Eulero Implicito

Assoluta Stabilità (A-Stability) per Eulero Implicito

Metodo dei Trapezi o Metodo di Crank-Nicolson

Sii il primo a commentare

Lascia un commento Annulla risposta